Kalkulator logarytmów umożliwia obliczanie logarytmów zarówno z pierwiastkami, jak i bez pierwiastków. Domyślnie obliczane są logarytmy bez pierwiastków, z możliwością liczenia liczb dodatnich i liczby e. Po kliknięciu „pokaż zaawansowane opcje” możliwe jest obliczanie logarytmów również z pierwiastkami. Często używanym przypadkiem logarytmu jest logarytm dziesiętny log₁₀(x). Drugim przykładem jest ln(x), który oznacza logarytm naturalny x, z podstawą w liczbie e, czyli log_e(x).

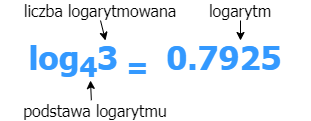
Podstawa logarytmu powinna być dodatnia, ponieważ logarytm z ujemną podstawą nie występuje w zbiorze liczb rzeczywistych.

Obliczanie logarytmów bez pierwiastków

Aby obliczyć logarytm bez pierwiastków, wystarczy wprowadzić liczbę, dla której chcemy obliczyć logarytm, oraz podać podstawę logarytmu. Następnie klikamy przycisk „Oblicz” i kalkulator wyświetli nam wynik.

Przykład:

Chcemy obliczyć logarytm o podstawie 10 dla liczby 100.

Wprowadzamy liczbę 100 jako „Liczba” oraz 10 jako „Podstawa logarytmu”. Kalkulator wyświetli nam wynik: 2.

Obliczanie logarytmów z pierwiastkami

Aby obliczyć logarytm z pierwiastkiem, należy skorzystać z zaawansowanych opcji kalkulatora. Po kliknięciu „pokaż zaawansowane opcje” pojawią się dodatkowe pola do uzupełnienia.

W polu „Liczba” wprowadzamy liczbę, dla której chcemy obliczyć logarytm z pierwiastkiem. W polu „Podstawa logarytmu” wprowadzamy podstawę logarytmu, a w polu „Pierwiastek” podajemy stopień pierwiastka.

Następnie klikamy przycisk „Oblicz” i kalkulator wyświetli nam wynik.

Przykład:

Chcemy obliczyć logarytm z pierwiastkiem stopnia 2 dla liczby 16.

Wprowadzamy liczbę 16 jako „Liczba”, 2 jako „Podstawa logarytmu” oraz 2 jako „Pierwiastek”.

Klikamy przycisk „Oblicz” i kalkulator wyświetli nam wynik: 4.

Kalkulator logarytmów a liczenie liczb dodatnich i liczby e

Kalkulator logarytmów umożliwia również obliczanie logarytmów dla liczb dodatnich oraz liczby e. Aby skorzystać z tej funkcji, wystarczy wprowadzić odpowiednią wartość w polu „Liczba”.

Przykład:

Chcemy obliczyć logarytm o podstawie e dla liczby 2.

Wprowadzamy liczbę 2 jako „Liczba” oraz e jako „Podstawa logarytmu”. Kalkulator wyświetli nam wynik: 0.6931.

Kalkulator logarytmów jest prostym narzędziem, które pozwala na szybkie obliczanie logarytmów zarówno z pierwiastkami, jak i bez pierwiastków. Dzięki temu narzędziu można łatwo sprawdzić wartość logarytmu dla różnych liczb i podstaw. Skorzystaj z kalkulatora logarytmów i przyspiesz swoje obliczenia!

Kalkulator logarytmów – zasady liczenia i wzory

Logarytm to jedno z podstawowych pojęć w matematyce, które często spotykamy w różnych dziedzinach nauki. Jest to funkcja odwrotna do potęgi, która pozwala nam rozwiązywać różnego rodzaju problemy związane z liczbami. Kalkulator logarytmów jest narzędziem, które pomaga nam obliczyć logarytm danej liczby.

Czym jest logarytm?

Logarytm to funkcja matematyczna, która mierzy, ile razy musimy podnieść pewną liczbę (nazywaną podstawą logarytmu) do pewnej potęgi, aby otrzymać daną liczbę. Oznaczamy go symbolem log.

Logarytmy są szczególnie przydatne w przypadkach, gdy mamy do czynienia z liczbami bardzo dużymi lub bardzo małymi. Dzięki nim możemy przekształcić operacje potęgowania na operacje dodawania i odejmowania, co znacznie ułatwia obliczenia.

Zasady liczenia logarytmów

Przejdźmy teraz do zasad liczenia logarytmów. Poniżej przedstawiamy najważniejsze reguły, które warto znać:

1. Właściwości podstawy logarytmu

Podstawą logarytmu może być dowolna liczba dodatnia, z wyjątkiem 1. Najczęściej używanymi podstawami są liczby 10 (logarytm dziesiętny) i e (logarytm naturalny).

2. Logarytm z iloczynu

Logarytm z iloczynu dwóch liczb jest równy sumie logarytmów tych liczb. Matematycznie można to zapisać jako:

log_b(a * c) = log_b(a) + log_b(c)

3. Logarytm z ilorazu

Logarytm z ilorazu dwóch liczb jest równy różnicy logarytmów tych liczb. Matematycznie można to zapisać jako:

log_b(a / c) = log_b(a) – log_b(c)

4. Logarytm z potęgi

Logarytm z liczby podniesionej do potęgi jest równy iloczynowi potęgi i logarytmu tej liczby. Matematycznie można to zapisać jako:

log_b(aⁿ) = n * log_b(a)

5. Logarytm z pierwiastka

Logarytm z pierwiastka z liczby jest równy ilorazowi logarytmu tej liczby i stopnia pierwiastka. Matematycznie można to zapisać jako:

log_b(√a) = log_b(a) / 2

Wzory logarytmiczne

Przejdźmy teraz do najważniejszych wzorów logarytmicznych, które warto znać:

1. Wzór logarytmu dziesiętnego

Logarytm dziesiętny liczby a jest równy logarytmowi naturalnemu tej liczby podzielonemu przez logarytm naturalny podstawy 10. Matematycznie można to zapisać jako:

log₁₀(a) = ln(a) / ln(10)

2. Wzór logarytmu naturalnego

Logarytm naturalny liczby a jest równy logarytmowi dziesiętnemu tej liczby podzielonemu przez logarytm dziesiętny podstawy e. Matematycznie można to zapisać jako:

ln(a) = log_e(a) / log_e(10)

3. Wzór logarytmu potęgowego

Logarytm potęgowy liczby a o podstawie b jest równy logarytmowi naturalnemu liczby a podzielonemu przez logarytm naturalny liczby b. Matematycznie można to zapisać jako:

log_b(a) = ln(a) / ln(b)

Mamy nadzieję, że powyższe informacje pomogły Ci zrozumieć zasady liczenia logarytmów oraz zapoznać się z najważniejszymi wzorami. Logarytmy są niezwykle przydatne w matematyce i naukach przyrodniczych, a ich znajomość może ułatwić rozwiązywanie różnego rodzaju problemów.